The Beautiful Game:

This is Physics Professor Metin Tolan, of the University of Dortmund. Dr. Tolan gives lectures about the physics of football to packed audiences, where he explains how banana kicks work, and often spins off about the impossibility of certain things in film (such as James Bond magnetically undoing zippers, or certain aspects of Star Trek).

Lately, he has been on dozens of interviews for news shows all over the world. He has done a statistical calculation with some interesting results, especially during this football-crazed time, and epecially for his football-crazed nation.

It turns out that Bessel functions are a good fit to professional football (soccer) scoring statistics, and Tolan has used them to calculate the odds for the current World Cup teams. After analyzing thousands of games, it seems that the scoring rate of national teams is not particularly dependent on who is on the field, who is the coach, or several other factors one might think are important (ssshhh, don't tell the players, agents or fans). As Kim Allen points out in his blog on Tolan, "In a single sweep, he dismisses the entire field of sports psychology." Apparently, the two major contributors to scoring rate are nationality and whether you are playing at home or not.

Tolan carried out two calulations: one to get the odds of winning for each team at this particular World Cup, and one to match the performance of the German team over time. His match to Germany's past and predicted performance is obviously what is catching the attention of the Germans, as in this graph of the function:

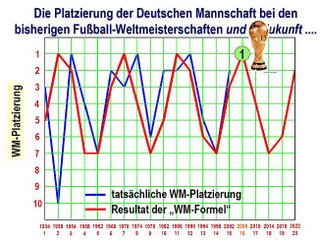Where blue is the actual placing of the team over all the past World Cups, and red is the result of the WM-Formal model in this crude graphic of Germany's team placement over time. I have several issues with this whole approach (as does Tolan himself, he admits freely), but of course the press brushes off these cautions. "Physics ensures the Cup is ours!"

The interesting part for me was that he had approximated each team as a Poisson emitter (kind of like a radioactive element). Without the home team advantage, Germanium has only a 10.69% chance of winning, while Brazilium is the favourite, with a 15.56% chance. Now, the home team advantage is somewhere between 1 and 2 goals per game, which increases Germany's chances to 33.18% if the advantage is one goal, and to a whopping 56.39% chance if the advantage is an unlikely 2 goals per game. Those are betting odds!

And Tolan, like any competent statistician, has an interest in gambling. He not only deals with World Cup football, but he looks at things like card shuffling machines for weaknesses. He says his money is on Germany - but then he also knows his emotions are involved, and those tend to cloud any results from beautiful formulae. ...he has also lost bets too, losing a favourite football uniform from a Bavarian football team to a friend.

And those formulas on the chalkboard behind him? Real - but probably only because Spiegel took the photo on Tolan's home turf. There are some other efforts to get real math out into public view - the current CBS show Numb3rs, where my old statistics prof Gary Lorden serves as a consultant to ensure the references to math in the script and on the chalkboards in that show are correct. Gary also had an interest in gambling - enough to be blacklisted at every major casino in Vegas for his successful counting schemes, based on... math.

OK, I've got my lucky Brasil #9 Ronaldo jersey on (four stars only, from before the 2002 WC win), and I'm bouncing up and down waiting for the kick-off whistle. And I've got my bets backed up by a formula. Hope I don't lose that whole dollar...

Theme spotted in Toni Feder's Physics Today 26 June article, and supplemented by:

• A Spiegel article (in German)


• An interview on "As it Happens" from CBC Radio: http://www.cbc.ca/radioshows/AS_IT_HAPPENS/20060608.shtml

(...and you thought the James Bond link was going to be video, and not just a German podcast. Heh.)

Can't see the Forest:

Thanks to Grant Hutchinson's Flickr page, I found this nice Java app that maps out website trees. You type in an URL, and watch the tree grow. Fascinating.

http://www.aharef.info/static/htmlgraph/

Here's this blog's (::dura:mater::'s) map:



What do the colors mean?

blue: links (a tags)
red: tables (table, tr, td tags)
green: divs
violet: images (img tags)
yellow: forms (form, input, textarea, select, option tags)
orange: block formatting (br, p, blockquote tags)
black: root (html tag)
gray: all other tags

My only wish is that one could point and click to get info about a particular node ("what is this one?").

So this got me thinking about all the fuss that is made over simplifying agency web-sites in the US government, and this was a chance to put a certina sub-set to the test.

See if you can guess which one is which. Match the numbers in the list with the letters for the trees. Do they match your impression of organization at the relevant organization?

1. National Science Foundation (NSF)
2. Department of Defense (DOD)
3. National Oceanic and Atmospheric Administration (NOAA)
4. National Institutes of Health (NIH)
5. Central Intelligence Agency (CIA)
6. State Department
7. Energy (DOE)
8. NASA
9. Geological Survey (USGS)
10. The White House

A:

B:

C:

D:

E:

F:

G:

H:

I:

J:

No, there's no answer key - that's what that link up top is for...

There are some definite surprises (I, for example), and some obvious ones (G, at least for me it was).

Lost World:

...or Sir Arthur Conan Doyle takes out his looking glass, and investigates the Guyana Highlands of South America.

I was lucky enough to complete one of my lifetime quests last week. I got to see Angel Falls. And I want to go and do it again, this time on foot, from the top. This post is a series of pictures that will focus in on this remnant of an ancient landscape.

The first diagram here shows South America, as seen by the Shuttle Radar Topography Mission (SRTM). Color indicates height, as on most maps. Shading is controlled by radar reflectance, a rather complicated topic I will leave for another post. The red box is the area blown up in the next map.

If you click on the picture itself, you will go to an index page where you can download the full resolution picture (a whopping 7.8Mb JPEG, 7,200x10,886 pixels).

The next picture focuses on the Guyana Highlands area outlined in red above - a set of enormous mesas that rise 2,000 to 3,000 feet above the savannas of Venezuela, Guyana and Brazil. The mesas, known as tepuis, were formed over hundreds of millions of years as rivers cut into a thick layer of pink quartzite sandstone, itself as old as the Precambrian. The contrast between the dark green mantle covering the tepui tops, the sheer pink and black cliffs, and the lighter green to brown savannas is stunning. Most of the higher tepuis in this image have never been visited by a human. They are almost impossible to get to, even by helicopter. There are very few places left on Earth like that. The red circle outlines Auyán Tepui, from which Angel Falls ...fall.

Again, if you click on the picture itself, you will go to an index page where you can download the full resolution picture (1,900x1,070 pixels), which includes a version of the best known topography before SRTM was flown.

Now we switch to Google Earth for the next inwards zoom, and focus on the Auyán Tepui area itself. You can match the heart-shaped area in the center of this picture to the shape seen in the above radar picture to orient yourself. The red circle here indicates the central canyon through the tepui, cut by innumerable waterfalls that line the canyon walls. The red rectangle outlines the next zoom, into the Canaima area where flights land.

If you click on this picture, you will get a larger version without the red markings.

In this picture of the Canaima area, the red circle outlines a tepui I will come back to below. The red rectangle is an area that I photographed obliquely from the air, shown below.

Again, if you click on this picture, you will get a larger version, without the red markings.

In the aerial photo below, looking roughly West, you should be able to match up the channels of the Carrao River with the "tines" visible in the center-top of the red rectangle area. You can just make out the Canaima (CAJ/SVCN) landing strip in the oblique aerial photo, and the strip is quite clear in the center-left border area of the rectangle in the Google Earth photo. The landing strip was crushed gravel - FOD city, which made for a noisy landing and take-off.

And clicking on this picture will take you to my Flickr page for it...

This next photo was taken from the Western shore of the Canaima Lagoon (actually still part of the Carrao River) at the "elbow" to the left of the tines, looking North-East towards the red-circled tepui I referred to above (this is called Karavaina Tepui). If you look carefully, you can see that there are lower, sloping tepuis to the left and right in this picture, which can also be made out as triangluar blocks in the Google Earth picture above (they are known as the Nonoy and Topuchi Tepuis). The waterfalls here were spectacular, even for being the end of the dry season. There is enough space behind them for multiple groups of fat tourists. The water is quite red from the tannins, and the "beaches" in the area are distinctly pink from the rose quartzite.


This next picture is an aerial photo of Karavaina Tepui, typical of one of the lower tepui structures - sheer walls surrounded by a debris pile, with a relatively, but not completely flat, top. Taller tepuis will have double or triple stacks of these cliff-debris combinations. Most of the tepuis have extremely rough, or karstic terrain on their tops - highly dissolved rock full of caves and pits. This leads to some amazing places for caving, but the truly marvelous oddity is that this type of terrain usually occurs in calcareous stone like limestone. These layers have been here for so long (longer than almost anywhere else on Earth) that water has been able to perform its erosive magic even through quartz sandstone. This landscape has escaped the violence of tectonics and lain still since before the dinosaurs were a twinkle in Nature's eye. The isolation from the surrounding territory has also allowed the tepui tops to develop their own peculiar ecosystems - some of them have their own specific species of plants, frogs, etc. Here's a nice intro with some depth to it...


But this isolation might also be the ecosystems' undoing - as global warming occurs, species usually adapt by moving upslope, following the isotherms. On a tepui, there is literally nowhere to go. However, I note that given the length of time these structures have been here - this type of thing has happened before. Here's a group that has just started looking at this issue - I plan to meet one of them later this year in Beijing. It is this 'splendid isolation' that led many biologists in the late 1870's (just after Darwin's "Origin of the Species" and "Descent of Man" were published) to speculate that the tepuis might harbour species long extinct elsewhere - perhaps even dinosaurs. An expedition in 1882 led by Everard Im Thurn finally ascended to the 9,000 foot summit of Roraima Tepui, and Sir Arthur Conan Doyle supposedly attended one of the lectures the expedition gave on their return, and his book "The Lost World" was (probably) the result. From there, Michael Crichton and Steven Spielberg moved all this mythology northwards and onto Pacific islands off the coast of Costa Rica.

From Canaima we flew in a 15-seater high wing into the canyon of Auyán Tepui, sandwiched from below by fog, and above by low stratus clouds that covered the top of the tepui. All we could see was the sides of the canyon, which were lined with waterfall after waterfall, spilling the rains that fall on the moister tops into the drier valleys below. The pilot announced that they were not sure it was clear enough to see the falls themselves, and an audible groan cut through the drone of the engines. But my wish was strong enough to part the clouds, and suddenly there it was. For a few seconds we showed our plane's belly as the pilot put us into a very tight turn inside the canyon, and both sides of the aisle had seen the unimaginably slow drops of water falling 3,212 feet -- much like Jimmy Angel and his crew did in 1933.

I sat happily on the way home, smiling as I gazed out over the "Great Savanna," and the slowly hazier air as we flew back North into the "real" world.

Additonal Links:

• The Lost World
  
• A modern (1994) trip up Roraima Tepui
  
• Trekking on the cheap
  
• Nice photo gallery

Martian Dust Devils:

I found this animated GIF the other day while trying to locate stuff for my son about Mars.

It reminded me that I had had a conversation a few months ago with an old friend from grad school, Nilton Rennó, about his research work, and he told me he was busy working on the electrical properties of small eddies like these dust devils. It turns out that these things generate very intense electrical fields, and that this potential makes a large amount of dust jump off the surface, to be carried away and up into the air. His take was that these small phenomena contribute a lot more to suspended aerosols than we currently take into account.

From the NASA Phoenix mission page that has a description of his work:

Recently, Renno and his collaborators found evidence of large electric fields and non-thermal microwave emission by Martian dust devils and dust storms (Renno et al. 2003). They also showed that convective plumes and vortices play a very important role in the Earth?s aerosol budget (Renno et al. 2004, Koch and Renno 2004). Indeed, graduate student Jacquelin Koch recently showed that convective plumes and vortices are responsible for more than 20% of the terrestrial aerosol budget. In addition, Renno and his collaborators have been studying the electrification of terrestrial and Martian dust devils and storms and their effects on dust lifting and atmospheric chemistry. They have already shown that, on Mars dust electrification leads to the formation of large quantities of H2O2, a powerful oxidant. This has important implications for the chemistry of the martian soil and perhaps even to its hydrological cycle.